Наибольший общий делитель и наименьшее общее кратное.

В этом уроке мы поговорим о том как вычислять НОД и НОК. Дело в том, что элементарные арифметические вычисления должен уметь делать любой программист, так как алгоритм вычисления можно встретить во многих программах. Тем более вы их уже должны знать, если вы учились в школе 5 классе.

Наибольший общий делитель. НОД.

Для нахождения общего делителя вам нужно знать следующее:

Запомните: наибольший общий делитель (НОД) двух целых чисел – это наибольшее целое число, на которое делятся оба исходных числа без остатка. Однако одно из исходных чисел должно быть большее нуля.
Запомните: если у вас одно из двух чисел ноль, то НОД будет, то число что больше ноля.
Запомните: существует понятие взаимно-простых чисел, у которого нет общих делителей, кроме единицы. К примеру число 5 и 4, НОД этих чисел будет равен 1, так как если 5 разделить на 4 вы не получите целое число без остатка, следовательно НОД=1

Все остальные числа, у которых НОД больше 1, вычисляются по принципу бинарного алгоритма или с помощью алгоритма Евклида. В этой статье мы подробно разберем алгоритм Евклида, который еще называют взаимным вычитанием, поскольку НОД получается при последовательном вычитании меньшего из большего. Используем алгоритм Евклида в нашем примере НОД(12, 30). По алгоритму Евклида нам надо вычесть из большее меньшее, то есть из 30-12-12=6 В числе 30 у нас может поместиться число 12 только два раза, число 12 называют кратным, и остатком останется число 6. Теперь нам надо из числа 30 отнять кратное числа 6, которое у нас получилось, 30-6-6-6-6-6=5 НОД числа 12 и 30 будет равен 6. Так как нам надо найти именно наибольший делитель в нашем случаи 6 больше 5, следовательно НОД(12,30)=6. Как видите ничего сложного, теперь давайте составим блок схему.

Блок-схема «Алгоритм Евклида»

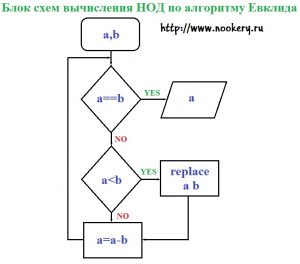
рис.1

Если число a и b равно, НОД этих чисел будет любое из них, так как они могут делиться друг на друга. Если a и b не равны, мы их сравниваем a<b, если a меньше чем b то их надо поменять местами в a присвоить значение b, в b присвоить значение а и перейти к следующему вычислению описанного ниже. Если a больше чем b то, надо из а вычесть b, результат сохранить в a, и так до тех пор, пока а не станет равно b. Рассмотрим на примере.

Пример НОД(12,30).

12=30 | a==b; //в нашем случаи 12 не равно 30
12<30 | a<b;//производим сравнение на < >
30 12 | a==b; b==a; //меняем местами
30-12=18 | a=a-b;//производим вычитание
18=12| a==b;//равно ли а и b
18<12| a<b; //в нашем случае а >b
18-12=6|a=a-b; //производим вычитание
6=12|a==b; //в нашем случаи 6 не равно 12
6<12|a<b; //производим сравнение на < >
6 12| a==b; b==a; //меняем местами
12-6=6|a=a-b;//производим вычитание
6=6| a==b; //в нашем случаи 6 равно 6
НОД(12,30)=6;

Наименьшее общее кратное(НОК).

НОК-это число которое из двух и более натуральных чисел является наименьшим натуральным числом, которое само делится нацело, и каждое из исходных чисел.

Самый простой и быстрый способ в плане реализации программного кода, это первоначально вычислить НОД двух чисел, затем произведение исходных двух целых чисел a и b разделить на НОД. Посмотрим на примере как это выглядет. Возьмем за пример все те же цифры 12 и 30 как мы помним наибольшее общее кратное равнялось 6. НОД=6 Следовательно по формуле НОК=a*b/НОД. НОК=12*30/6=60 Есть и другие варианты вычисления НОК к примеру каноническое разложение чисел. Рассмотрим пример, первоначально нам надо выяснить какое из чисел больше, потом мы раскладываем числа на кратные 12=2*2*3 , и число 30=2*3*5 Вычисляем произведение кратных чисел из числа 30, так как оно является наибольшим. В следующей операции, одинаковые цифры вычеркиваются, как это сделал я из большего меньшее, а оставшиеся кратные числа из 12 умножаются друг на друга, у нас осталось только число 2, которое умножается на произведение кратных чисел из 30, в результате вычисления вы и получите НОК. Выглядет это следующим образом НОК=2*3*5*2=60 Хорошо это можно представить в виде столбиков, как это можно видеть из рис. 2.

рис. 2

В целом ничего сложного, главное не запутаться, сейчас мы нарисуем блок схему наименьшего общего кратного (НОК).

Блок схема Наименьшего общего кратного (НОК)

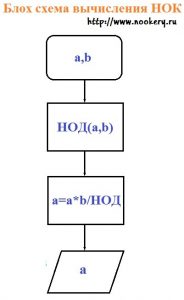рис 3.

Алгоритм работы программы описан вначале, статьи о НОК.

Но как же быть если нам надо к примеру найти НОД трех и более натуральных чисел, или найти НОК трех или более натуральных чисел. Тут ничего сложного инструкцию по нахождению НОД из 3 чисел и НОК смотрим ниже.

НОД трех чисел:

Сравниваем все числа К примеру a<b<c
Начинаем вычисления с больших чисел к меньшим
Вычисляем НОД по аналогии с двумя числами a и b
Вычисляем по аналогии чисел НОД(a,b) и с Пример: НОД(a,b,c)=НОД((НОД(a,b)),с);
НОД(12,30,60)
12<30<60
НОД(60,30)=30
НОД(30,12)=6

Точно так же производиться вычисления НОД из четырех чисел из пяти итд. По аналогии с НОД вычисляется и НОК с тремя и более числами. Приведу в пример НОД трех чисел блок схему алгоритма смотрите рис. 4.

Блок схема НОД алгоритма трех чисел, четырех чисел итд.

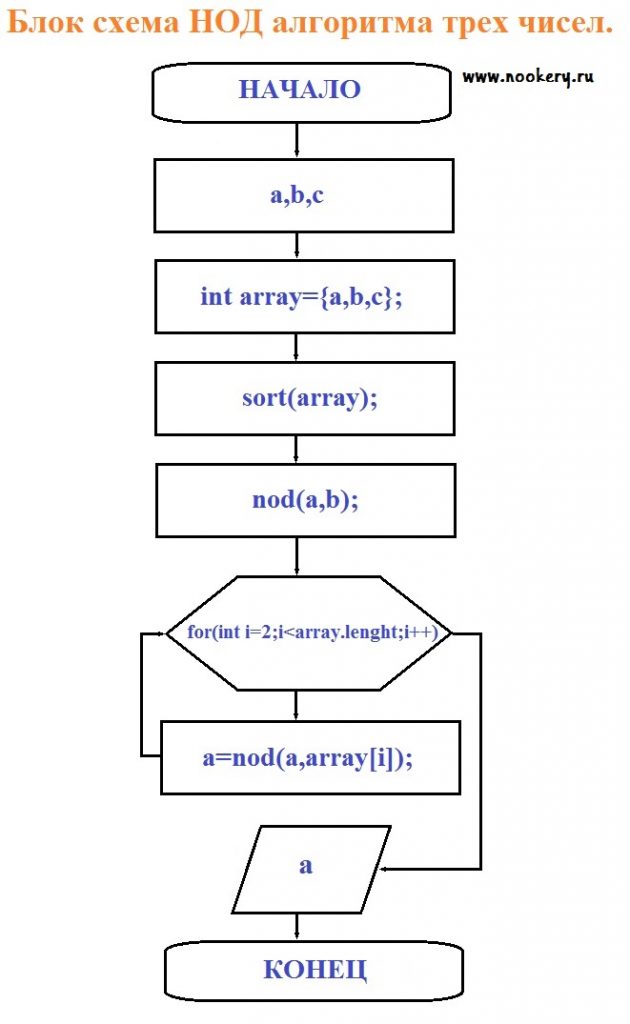
рис. 4

Разберем по подробнее работу программы блок схемы из рис. 4.

У нас подается 3 числа, но их может быть сколько угодно.
Их мы записываем в массив array.
Выполняем метод sort(); Это мой метод он принимает массив чисел, делает сортировку по убыванию, пузырьковым методом, о нем вы можете прочитать из уроков о массивах.
Выполняем метод nod(), который принимает первые два числа. Я создал метод по аналогии как написано выше в этой статье.
В следующем блоке я помещаю в тело цикла метод nod(), который присваиваю возвращаемое число из метода nod() переменной a.
Выводим результат.
Завершаем работу программы.

Скачать калькулятор НОК и НОД .

Пока писал статью, написал программу НОК и НОД вычисления, которую можете скачать с сайта. Работа программы очень простая, достаточно в текстовое поле вписать цифры через пробел или запятую, нажать на кнопку вычислить или Enter и программа выведет результат. Программа написана на языке java. Может запускаться со всех систем.

рис 5.

Скачать калькулятор НОК и НОД .