Приветствую всех, сегодня рассмотрим алгоритм построения, поиска, удаления, и обхода двоичного дерева.
Двоичное дерево — древовидная структура данных, в которой каждый узел имеет не более двух потомков (детей). В такой структуре первый узел называется родительским узлом, а дети называются левым и правым потомками соответственно.
Двоичное дерево поиска (binary search tree, BST) — это двоичное дерево, для которого выполняются следующие условия:
- Оба поддерева — левое и правое, являются двоичными деревьями поиска.
- У всех узлов левого поддерева произвольного узла «A» значения ключей меньше, нежели значение ключа самого узла «A».
- В то время, как у всех узлов правого поддерева того же узла «A» значения ключей не меньше, нежели значение ключа узла «A».
- Очевидно, данные в каждом узле должны обладать ключами, для которых определена операция сравнения.
Двоичное дерево поиска можно определить так:
- Каждое новое поддерево (левое и правое) являются двоичными деревьями поиска.
- У всех узлов левого поддерева значения ключей меньше, чем значение ключа элемента родителя.
- У всех узлов правого поддерева значения ключей не меньше, чем значения ключа родительского узла.
Основным преимуществом двоичного дерева поиска перед другими структурами данных является высокая эффективность реализации основанных на нём алгоритмов поиска и сортировки.
Реализация двоичного дерева поиска начинается с задания узла, который содержит ссылки на свой левый и правый потомок, если они у него есть. При добавлении нового узла в дерево, его значение сравнивается с помощью метода IComparable.CompareTo со значением родительского элемента, что бы определить правый это потомок или левый.
|
1 2 3 4 5 6 7 8 9 |
class BinaryTreeNode<TNode> : IComparable<TNode> where TNode : IComparable<TNode> { public BinaryTreeNode<TNode> Left { get; set; } public BinaryTreeNode<TNode> Right { get; set; } public int CompareTo(TNode other) { return this.CompareTo(other); } } |
Метод добавления нового узла в дерево:
Алгоритм добавления нового узла в дерево не сложен и значительно упрощается с применением рекурсии. Если дерево не содержит узлов (пустое), то новое значение становится корнем нового дерева. Если дерево не пустое, то мы сравниваем значение нового узла со значением корня дерева, если новое значение больше, то алгоритм повторяется для правого потомка, если меньше то для левого.
|
1 2 3 4 5 6 7 |
public class BinaryTree<T> : IEnumerable<T> where T : IComparable<T> { public void Add(T value) { // } } |
Метод поиска узла:
Поиск узла в дереве начинается с его корня (метод FindWithParent) и предполагает следующие шаги:
- Если значения текущего узла null — закончить поиск и вернуть null.
- Если значения текущего узла равно искомому, результатом поиска будет текущие значение узла.
- Если искомое значение меньше чем текущие, нужно перейти к левому потомку и повторить алгоритм с первого пункта.
- Если значение больше или равно текущему, нужно перейти к правому потомку и повторить алгоритм с первого пункта.
Метод Contains() основывается на методе поиска и определяет принадлежит ли указанный элемент дереву или нет, если да то он возвращает true, в противном случае false.
Удаления узла дерева:
При удалении узла из дерева нужно учитывать три возможных варианта:
- Первый вариант: удаляемый узел не имеет правого потомка.
- Второй вариант: удаляемый узел имеет правого потомка, у которого нет левого потомка.
- Третий вариант: удаляемый узел имеет правого потомка, у которого есть левый потомок.
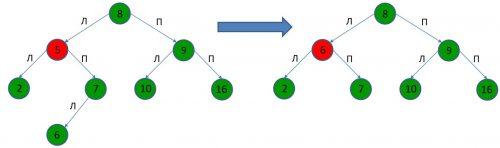
1. Если удаляемый узел(5) не имеет правого потомка, то достаточно переместить на его место левого потомка(2).
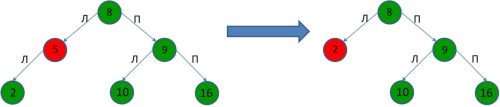
2. Если удаляемый узел(5) имеет правого потомка(6), у которого в свою очередь, тоже есть правый потомок(7), то достаточно переместить их с соблюдением иерархии.
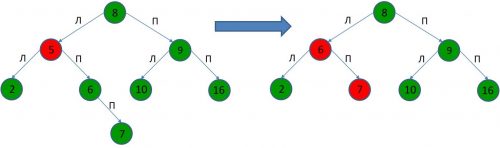
3. Если удаляемый узел (5) имеет правого потомка (7), у которого в свою очередь есть левый потомок(6), то крайний левый потомок узла (7) должен быть перемещен на место удаляемого узла.
Алгоритм обхода
Алгоритм обхода двоичного дерева предусматривает обход всех вершин дерева только один раз.
Существуют три вида таких обходов:
Прямой порядок (англ. preorder), посещение узлов родителей до посещения узлов потомков:
- Зайти в корень.
- Зайти в левое поддерево.
- Зайти в правое поддерево.
Обратный порядок (англ. postorder), посещение узлов потомков до посещения узлов их родителей:
- Зайти в левое поддерево.
- Зайти в правое поддерево.
- Зайти в корень.
Симметричный порядок(англ. inorder):
- Зайти в левое поддерево.
- Зайти в корень.
- Зайти в правое поддерево.
Прямой порядок
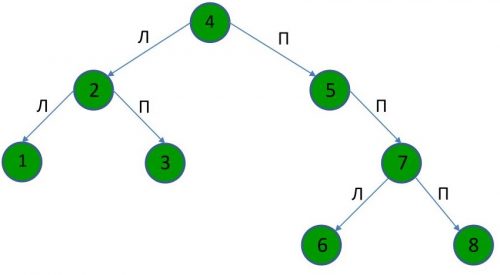
Порядок следования при прямом обходе дерева: 4, 2, 1, 3, 5, 7, 6, 8
Обратный порядок
Порядок следования при обратном обходе дерева: 1, 3, 2, 6, 8, 7, 5, 4
Симметричный порядок
Порядок следования при обратном обходе дерева: 1, 2, 3, 4, 5, 6, 7, 8