Приветствую всех, тема довольно сложна для понимания, и требует вашей концентрации внимания.
АВЛ-дерево – сбалансированное по высоте двоичное дерево поиска. Было названо в честь советских учёных Адельсона-Вельского Георгия Максимовича и Ландиса Евгения Михайловича, которые впервые описали алгоритм и его структуру. Правила построения двоичных деревьев поиска:
- каждый узел может иметь не более двух потомков (левый и правый);
- значения которые меньше текущего размещаются в левом поддереве;
- значения которые больше или равные текущему размещаются в правом поддереве;
Дополнительное условие для АВЛ-дерева:
- для любого узла дерева, высота его правого поддерева никогда не превышает высоты его
левого поддерева более чем на единицу.
*Этого свойства достаточно, чтобы высота дерева имела логарифмическую зависимость от
числа его узлов.
Узел «6» не имеет родительского узла, поэтому он является корнем дерева и находится на первом уровне. Узлы «4» и «8» это братские узлы, которые находятся на втором уровне. Узлы «3» и «5» находятся на третьем уровне. Используя эти уровни, можно найти расстояние между узлами «6» и «3», оно равно двум.
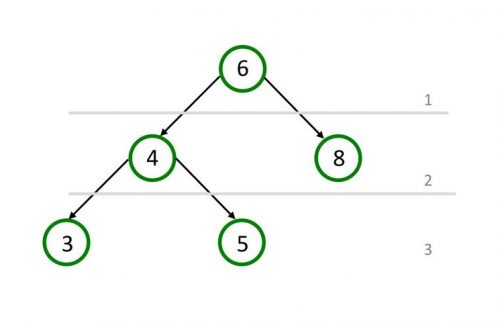
Не сбалансированное дерево
Минимальная высота левого и правого поддерева не может отличатся больше чем на единицу и это правило характерно для всех узлов дерева. Если рассмотреть корень узла, то его левое поддерево имеет высоту два, а правое – ноль, поэтому дерево не сбалансировано.
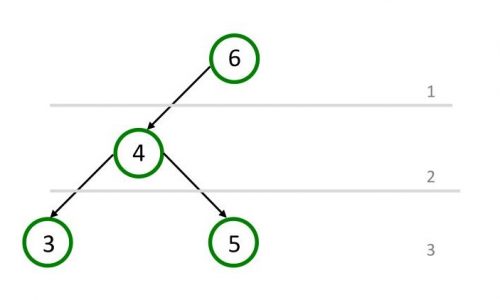
Частично сбалансированное дерево
Дерево называется полностью сбалансированным, если каждый узел дерева сбалансированный. Узел «7» не сбалансированный, поскольку высота правого поддерева два, а левого – ноль.
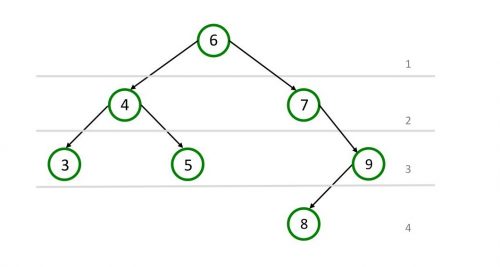
Алгоритм балансировки
Для определения сбалансировано дерево по высоте или нет, требуется проверить высоту правого и левого потомка каждого узла. При необходимости балансировки, узлы подлежат удалению, добавлению или вращению.
АВЛ-деревья используют базовые алгоритмы вращения узла:
- правое вращение,
- левое вращение,
- два смешанных алгоритма, которые базируются на первых двух.
Существуют четыре типа вращения:
- вращение влево,
- вращение вправо,
- вращение влево,
- а потом в право и в обратной последовательности.
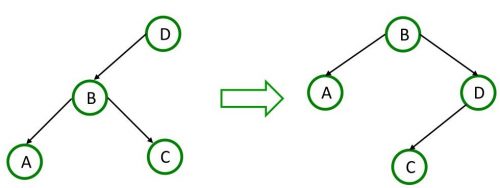
Вращение узла вправо
Алгоритм вращения вправо имеет три шага:
- земенить текущий корень на его левого потомка; узел B становится корнем, а узел А занимает его место.
- переместить правого потомка нового корня на место левого потомка старого корня. B -> C to D -> C.
- Присвоить новому корню (B) в качестве правого потомка старый корень (D).
Вращение узла влево
Алгоритм вращения влево осуществляется в три шага:
- земенить текущий корень на его правого потомка; узел «С» становится корнем, а узел «А» его левым потомком.
- переместить левого потомка нового корня (B) на место правого потомка старого корня. «С» -> «B» to «A» -> «B».
- Присвоить новому корню (С) в качестве правого узла значение старого корня (D).
Вращение вправо и влево
Данная ситуация отличается от предыдущих, поскольку правый потомок корня имеет левого потомка, но не имеет правого.
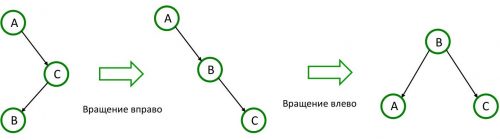
Вращение влево и вправо
Когда корень дерева имеет левого потомка, который в свою очередь имеет правого потомка, но не имеет левого, применяют последовательной вращения влево, а затем вправо.
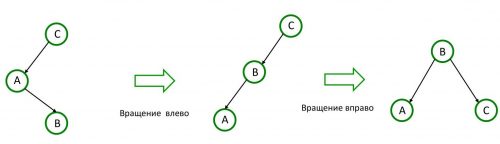
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 |
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace AVLTreeNode { // Класс AVLTreeNode реализует один узел АВЛ дерева public class AVLTreeNode<TNode> : IComparable<TNode> where TNode : IComparable { AVLTree<TNode> _tree; AVLTreeNode<TNode> _left; // левый потомок AVLTreeNode<TNode> _right; // правый потомок #region Конструктор public AVLTreeNode(TNode value, AVLTreeNode<TNode> parent, AVLTree<TNode> tree) { Value = value; Parent = parent; _tree = tree; } #endregion #region Свойства public AVLTreeNode<TNode> Left { get { return _left; } internal set { _left = value; if (_left != null) { _left.Parent = this; // установка указателя на родительский элемент } } } public AVLTreeNode<TNode> Right { get { return _right; } internal set { _right = value; if (_right != null) { _right.Parent = this; // установка указателя на родительский элемент } } } // Указатель на родительский узел public AVLTreeNode<TNode> Parent { get; internal set; } // значение текущего узла public TNode Value { get; private set; } // Сравнивает текущий узел по указаному значению, возвращет 1, если значение экземпляра больше переданного значения, // возвращает -1, когда значение экземпляра меньше переданого значения, 0 - когда они равны. #endregion #region CompareTo public int CompareTo(TNode other) { return Value.CompareTo(other); } #endregion #region Balance internal void Balance() { if (State == TreeState.RightHeavy) { if (Right != null && Right.BalanceFactor < 0) { LeftRightRotation(); } else { LeftRotation(); } } else if (State == TreeState.LeftHeavy) { if (Left != null && Left.BalanceFactor > 0) { RightLeftRotation(); } else { RightRotation(); } } } private int MaxChildHeight(AVLTreeNode<TNode> node) { if (node != null) { return 1 + Math.Max(MaxChildHeight(node.Left), MaxChildHeight(node.Right)); } return 0; } private int LeftHeight { get { return MaxChildHeight(Left); } } private int RightHeight { get { return MaxChildHeight(Right); } } private TreeState State { get { if (LeftHeight - RightHeight > 1) { return TreeState.LeftHeavy; } if (RightHeight - LeftHeight > 1) { return TreeState.RightHeavy; } return TreeState.Balanced; } } private int BalanceFactor { get { return RightHeight - LeftHeight; } } enum TreeState { Balanced, LeftHeavy, RightHeavy, } #endregion #region LeftRotation private void LeftRotation() { // До // 12(this) // \ // 15 // \ // 25 // // После // 15 // / \ // 12 25 // Сделать правого потомка новым корнем дерева. AVLTreeNode<TNode> newRoot = Right; ReplaceRoot(newRoot); // Поставить на место правого потомка - левого потомка нового корня. Right = newRoot.Left; // Сделать текущий узел - левым потомком нового корня. newRoot.Left = this; } #endregion #region RightRotation private void RightRotation() { // Было // c (this) // / // b // / // a // // Стало // b // / \ // a c // Левый узел текущего элемента становится новым корнем AVLTreeNode<TNode> newRoot = Left; ReplaceRoot(newRoot); // Перемещение правого потомка нового корня на место левого потомка старого корня Left = newRoot.Right; // Правым потомком нового корня, становится старый корень. newRoot.Right = this; } #endregion #region LeftRightRotation private void LeftRightRotation() { Right.RightRotation(); LeftRotation(); } #endregion #region RightLeftRotation private void RightLeftRotation() { Left.LeftRotation(); RightRotation(); } #endregion #region Перемещение корня private void ReplaceRoot(AVLTreeNode<TNode> newRoot) { if (this.Parent != null) { if (this.Parent.Left == this) { this.Parent.Left = newRoot; } else if (this.Parent.Right == this) { this.Parent.Right = newRoot; } } else { _tree.Head = newRoot; } newRoot.Parent = this.Parent; this.Parent = newRoot; } #endregion } } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 |
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace AVLTreeNode { public class AVLTree<T> : IEnumerable<T> where T : IComparable { // Свойство для корня дерева public AVLTreeNode<T> Head { get; internal set; } #region Количество узлов дерева public int Count { get; private set; } #endregion #region Метод Add // Метод добавлет новый узел public void Add(T value) { // Вариант 1: Дерево пустое - создание корня дерева if (Head == null) { Head = new AVLTreeNode<T>(value, null, this); } // Вариант 2: Дерево не пустое - найти место для добавление нового узла. else { AddTo(Head, value); } Count++; } // Алгоритм рекурсивного добавления нового узла в дерево. private void AddTo(AVLTreeNode<T> node, T value) { // Вариант 1: Добавление нового узла в дерево. Значение добавлемого узла меньше чем значение текущего узла. if (value.CompareTo(node.Value) < 0) { //Создание левого узла, если его нет. if (node.Left == null) { node.Left = new AVLTreeNode<T>(value, node, this); } else { // Переходим к следующему левому узлу AddTo(node.Left, value); } } // Вариант 2: Добавлемое значение больше или равно текущему значению. else { //Создание правого узла, если его нет. if (node.Right == null) { node.Right = new AVLTreeNode<T>(value, node, this); } else { // Переход к следующему правому узлу. AddTo(node.Right, value); } } //node.Balance(); } #endregion #region Метод Contains public bool Contains(T value) { return Find(value) != null; } /// <summary> /// Находит и возвращает первый узел который содержит искомое значение. /// Если значение не найдено, возвращает null. /// Так же возвращает родительский узел. /// </summary> /// /// <param name="value">Значение поиска</param> /// <param name="parent">Родительский элемент для найденного значения/// </param> /// <returns> Найденный узел (или ноль) /// </returns> private AVLTreeNode<T> Find(T value) { AVLTreeNode<T> current = Head; // помещаем текущий элемент в корень дерева // Пока текщий узел на пустой while (current != null) { int result = current.CompareTo(value); // сравнение значения текущего элемента с искомым значением if (result > 0) { // Если значение меньшне текущего - переход влево current = current.Left; } else if (result < 0) { // Если значение больше текщего - переход вправо current = current.Right; } else { // Элемент найден break; } } return current; } #endregion #region Метод Remove public bool Remove(T value) { AVLTreeNode<T> current; current = Find(value); // находим узел с удаляемым значением if (current == null) // узел не найден { return false; } AVLTreeNode<T> treeToBalance = current.Parent; // баланс дерева относительно узла родителя Count--; // уменьшение колиества узлов // Вариант 1: Если удаляемый узел не имеет правого потомка if (current.Right == null) // если нет правого потомка { if (current.Parent == null) // удаляемый узел является корнем { Head = current.Left; // на место корня перемещаем левого потомка if (Head != null) { Head.Parent = null; // убераем ссылку на родителя } } else // удаляемый узел не является корнем { int result = current.Parent.CompareTo(current.Value); if (result > 0) { // Если значение родительского узла больше значения удаляемого, // сделать левого потомка удаляемого узла, левым потомком родителя. current.Parent.Left = current.Left; } else if (result < 0) { // Если значение родительского узла меньше чем удаляемого, // сделать левого потомка удаляемого узла - правым потомком родительского узла. current.Parent.Right = current.Left; } } } // Вариант 2: Если правый потомок удаляемого узла не имеет левого потомка, тогда правый потомок удаляемого узла // становится потомком родительского узла. else if (current.Right.Left == null) // если у правого потомка нет левого потомка { current.Right.Left = current.Left; if (current.Parent == null) // текущий элемент является корнем { Head = current.Right; if (Head != null) { Head.Parent = null; } } else { int result = current.Parent.CompareTo(current.Value); if (result > 0) { // Если значение узла родителя больше чем значение удаляемого узла, // сделать правого потомка удаляемого узла, левым потомком его родителя. current.Parent.Left = current.Right; } else if (result < 0) { // Если значение родительского узла меньше значения удаляемого, // сделать правого потомка удаляемого узла - правым потомком родителя. current.Parent.Right = current.Right; } } } // Вариант 3: Если правый потомок удаляемого узла имеет левого потомка, // заместить удаляемый узел, крайним левым потомком правого потомка. else { // Нахожление крайнего левого узла для правого потомка удаляемого узла. AVLTreeNode<T> leftmost = current.Right.Left; while (leftmost.Left != null) { leftmost = leftmost.Left; } // Родительское правое поддерево становится родительским левым поддеревом. leftmost.Parent.Left = leftmost.Right; // Присвоить крайнему левому узлу, ссылки на правого и левого потомка удаляемого узла. leftmost.Left = current.Left; leftmost.Right = current.Right; if (current.Parent == null) { Head = leftmost; if (Head != null) { Head.Parent = null; } } else { int result = current.Parent.CompareTo(current.Value); if (result > 0) { // Если значение родительского узла больше значения удаляемого, // сделать крайнего левого потомка левым потомком родителя удаляемого узла. current.Parent.Left = leftmost; } else if (result < 0) { // Если значение родительского узла, меньше чем значение удаляемого, // сделать крайнего левого потомка, правым потомком родителя удаляемого узла. current.Parent.Right = leftmost; } } } if (treeToBalance != null) { treeToBalance.Balance(); } else { if (Head != null) { Head.Balance(); } } return true; } #endregion #region Метод Clear public void Clear() { Head = null; // удаление дерева Count = 0; } #endregion #region Итераторы public IEnumerator<T> InOrderTraversal() { // рекурсивное перемищение по дереву if (Head != null) // существует ли корень дерева { Stack<AVLTreeNode<T>> stack = new Stack<AVLTreeNode<T>>(); AVLTreeNode<T> current = Head; // при рекурсивном перемещении по дереву, нужно указывать какой потомок будет слудеющим (правый или левый) bool goLeftNext = true; // Начинаем с помещения корня в стек stack.Push(current); while (stack.Count > 0) { // Если перемещаемся влево ... if (goLeftNext) { // Перемещение всех левых потомков в стек. while (current.Left != null) { stack.Push(current); current = current.Left; } } yield return current.Value; // Если перемещаемся вправо if (current.Right != null) { current = current.Right; // Идинажды перемещаемся вправо, после чего опять идем влево. goLeftNext = true; } else { // Если перейти вправо нельзя - извлекаем родительский узел. current = stack.Pop(); goLeftNext = false; } } } } public IEnumerator<T> GetEnumerator() { return InOrderTraversal(); } System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator() { return GetEnumerator(); } #endregion } } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace AVLTreeNode { class Program { static void Main(string[] args) { AVLTree<int> Oak = new AVLTree<int>(); // 10 10 Oak.Add(10); // / \ / \ Oak.Add(3); // / \ / \ Oak.Add(2); // 3 12 ====> 3 15 Oak.Add(4); // / \ / \ / \ / \ Oak.Add(12); // 2 4 null 15 2 4 12 25 Oak.Add(15); // \ Oak.Add(11); // 25 Oak.Add(25); // Oak.Remove(11); foreach (var item in Oak) { Console.WriteLine(item); } Console.ReadKey(); } } } |
